RUMBO Y AZIMUT



Rumbo

El rumbo de una línea es el ángulo horizontal agudo (<90°) que forma con un meridiano de referencia, generalmente se toma como tal una línea Norte-Sur que puede estar definida por el N geográfico o el N magnético (si no se dispone de información sobre ninguno de los dos se suele trabajar con un meridiano, o línea de Norte arbitraria).
Como se observa en la figura, los rumbos se miden desde el Norte (línea ON) o desde el Sur (línea OS), en el sentido de las manecillas del reloj si la línea a la que se le desea conocer el rumbo se encuentra sobre el cuadrante NOE o el SOW; o en el sentido contrario si corresponde al cuadrante NOW o al SOE.
Como el ángulo que se mide en los rumbos es menor que 90° debe especificarse a qué cuadrante corresponde cada rumbo.

Por ejemplo en la figura las líneas mostradas tienen los siguientes rumbos:

Línea	RUMBO
OA	N30°E
OB	S30°E
OC	S60°W
OD	N45°W

Como se puede observar en la notación del rumbo se escribe primero la componente N o S del cuadrante, seguida de la amplitud del ángulo y por último la componente E o W.

Azimut

El azimut de una línea es el ángulo horizontal medido en el sentido de las manecillas del reloj a partir de un meridiano de referencia. Lo más usual es medir el azimut desde el Norte (sea verdadero, magnético o arbitrario), pero a veces se usa el Sur como referencia.
Los azimutes varían desde 0° hasta 360° y no se requiere indicar el cuadrante que ocupa la línea observada. Para el caso de la figura, las mismas líneas para las que se había encontrado el rumbo tienen el siguiente azimut:

Línea	AZIMUT
OA	30°
OB	150°
OC	240°
OD	315°

Contra-rumbo y Contra-azimut (Rumbo o azimut inverso)

Cuando se desea conocer la dirección de una línea se puede ubicar un instrumento para medirla en cualquiera de sus puntos extremos, por lo tanto se llaman rumbo y azimut inversos a los observados desde el punto contrario al inicial. Para que quede más claro, si en el ejemplo de la figura se midieron primero los rumbos y azimutes desde el punto O (líneas OA, OB, OC y OD), el contra-rumbo y contra-azimut de cada línea corresponde a la dirección medida en sentido opuesto, desde cada punto hasta O (líneas AO, BO, CO y DO).
Cuando se trata de rumbos, para conocer el inverso simplemente se cambian las letras que indican el cuadrante por las opuestas (N <-> S y E <-> W). De manera que para la figura se tiene:

Línea	RUMBO	CONTRA-RUMBO
OA	N30°E	S30°W
OB	S30°E	N30°W
OC	S60°W	N60°E
OD	N45°W	S45°E

Por el contrario, si se trata de azimutes, el inverso se calcula sumándole 180° al original si éste es menor o igual a 180°, o restándole los 180° en caso de ser mayor.

Contra-Azimut = Azimut ± 180°

Para la figura mostrada se observan los siguientes azimutes inversos:

Línea	AZIMUT	CONTRA-AZIMUT
OA	30°	30°+180° = 210°
OB	150°	150°+180° = 330°
OC	240°	240°-180° = 60°
OD	315°	315°-180° = 135°

Vale la pena volver a decir que en ningún caso un rumbo (o un rumbo inverso) puede ser mayor a 90°, ni un azi 

Vale la pena volver a decir que en ningún caso un rumbo (o un rumbo inverso) puede ser mayor a 90°, ni un azimut (o contra-azimut) mayor a 360°.

Conversión de Rumbo a Azimut

Para calcular azimutes a partir de rumbos es necesario tener en cuenta el cuadrante en el que se encuentra la línea. Observando la figura anterior se puede deducir la siguiente tabla:

Cuadrante	Azimut a partir del rumbo
NE	Igual al rumbo (sin las letras)
SE	180° – Rumbo
SW	180° + Rumbo
NW	360° – Rumbo

Se puede comprobar revisando los valores que aparecen en la figura.

Conversión de Azimut a Rumbo

Observando también la figura se ve que el cuadrante de la línea depende del valor del azimut así:

Azimut	Cuadrante	Rumbo
0° – 90°	NE	N ‘Azimut’ E
90° – 180°	SE	S ‘180° – Azimut’ E
180° – 270°	SW	S ‘Azimut – 180°’ W
270° – 360°	NW>	N ‘360° – Azimut’ W

mut (o contra-azimut) mayor a 360°.

Cálculo de Azimutes en poligonales

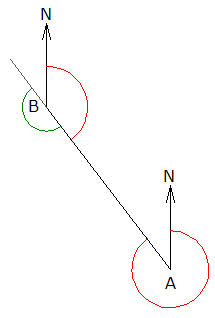
Una poligonal, sea abierta o cerrada, es una sucesión de distancias y direcciones (rumbo o azimut) formadas por la unión de los puntos en los que se armó el instrumento que se usó para medirlas (puntos de estación). Cuando se ubica el instrumento en una estación se puede medir directamente el azimut de la siguiente línea a levantar (si se conoce la dirección del N o si se “sostiene” el contra-azimut de la línea anterior), sin embargo, en ocasiones se mide el ángulo correspondiente entre las dos líneas que se intersectan en el punto de estación (marcando “ceros” en el ángulo horizontal del instrumento cuando se mira al punto anterior), a este último ángulo se le va a llamar “ángulo observado”.

Si el ángulo observado se mide hacia la derecha (en el sentido de las manecillas del reloj, que es el mismo en el que se miden los azimutes) se puede calcular el azimut de la siguiente línea con la siguiente expresión:

Azimut línea siguiente = Contra-azimut de la línea anterior + Ángulo observado

Se debe aclarar que si el resultado es mayor a 360° simplemente se le resta este valor.

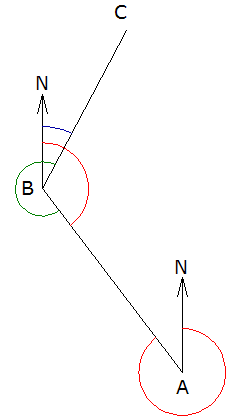
En la figura se observa que si el azimut conocido corresponde al de la línea AB (ángulo NAB en rojo), por lo tanto el contra-azimut es el ángulo NBA (también en rojo). El ángulo observado, medido en el sentido de las manecillas del reloj con el instrumento estacionado en el punto B es el ángulo ABC (en verde). El azimut que se desea conocer es el de la línea BC (ángulo NBC en azul). Por lo tanto se tiene la siguiente expresión:

Azimut BC = Contra-Azimut AB + Ángulo observado en B

Azimut BC =

Como es evidente que el resultado será mayor que 360° (en este caso en particular) entonces el azimut de la línea BC será:

Azimut BC = (

Esta expresión es válida sólo si el ángulo observado está medido en el mismo sentido del azimut (derecha), sin importar si es interno o externo.

Si se trata de calcular rumbos se pueden luego convertir los azimutes calculados de la forma anterior.

Notas

1. Wikipedia, la enciclopedia libre. Campo magnético terrestre

Bibliografía

Paul R. Wolf y Russel C. Brinker. Topografía. Novena Edición. Alfaomega. México, 1997